Partition problem
In computer science, the partition problem is an NP-complete problem. The problem is to decide whether a given multiset of integers can be partitioned into two "halves" that have the same sum. More precisely, given a multiset S of integers, is there a way to partition S into two subsets S1 and S2 such that the sum of the numbers in S1 equals the sum of the numbers in S2? The subsets S1 and S2 must form a partition in the sense that they are disjoint and they cover S. The optimization version asks for the "best" partition, and can be stated as: Find a partition into two subsets 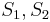 such that
such that 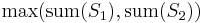 (or, equivalently, the difference between
(or, equivalently, the difference between 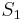 and
and 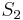 ) is minimized (sometimes with the additional constraint that the sizes of the two sets in the partition must be equal, or differ by at most 1).
) is minimized (sometimes with the additional constraint that the sizes of the two sets in the partition must be equal, or differ by at most 1).
The partition problem is equivalent to the following special case of the subset sum problem: given a set S of integers, is there a subset S1 of S that sums to exactly t /2 where t is the sum of all elements of S? (The equivalence can be seen by defining S2 to be the difference S − S1.) Therefore, the pseudo-polynomial time dynamic programming solution to subset sum applies to the partition problem as well.
A variation of the partition problem is the 3-partition problem, in which the set S must be partitioned into |S|/3 triples each with the same sum. In contrast to partition, 3-partition has no pseudo-polynomial time algorithm unless P = NP: 3-partition remains NP-complete even when using unary coding.
Contents |
Methods
Although the partition problem is NP-complete, there are heuristics that solve the problem in many instances, either optimally or approximately. For this reason, it has been called "The Easiest Hard Problem" by Brian Hayes.[1]
The pseudo-polynomial time dynamic programming solution for the subset sum problem applies to the partition problem as well, and gives an exact answer in polynomial time when the size of the given integers is bounded. In general, however, the numbers in the input may be exponential in the input size, and this approach may not be feasible.
One approach to the problem, imitating the way children choose teams for a game, is the greedy algorithm, which goes through the numbers in descending order, assigning each of them to whichever subset has the smaller sum. This works well when the numbers in the set are of about the same size as its cardinality or less. Another heuristic, due to Narendra Karmarkar and Richard Karp,[2] is the differencing algorithm, which at each step removes two numbers from the set and replaces them by their difference. This represents the decision to put the two numbers in different sets, without immediately deciding which one is in which set. The differencing heuristic performs better than the greedy one, but is still bad for instances where the numbers are exponential in the size of the set.[1]
Both heuristics have a running time of 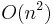 or less. The greedy algorithm is known to give a 4/3-approximation to the optimal solution of the optimization version. (In other words, if the greedy algorithm gives two sets
or less. The greedy algorithm is known to give a 4/3-approximation to the optimal solution of the optimization version. (In other words, if the greedy algorithm gives two sets 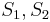 , then
, then 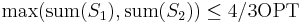 .) More generally, we can consider a version that takes the
.) More generally, we can consider a version that takes the  largest elements, and for each partition of them, extends the partition by adding the remaining elements successively to whichever set is smaller. (The greedy algorithm corresponds to
largest elements, and for each partition of them, extends the partition by adding the remaining elements successively to whichever set is smaller. (The greedy algorithm corresponds to 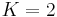 .) This version runs in time
.) This version runs in time 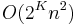 and is known to give a
and is known to give a 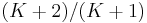 approximation; thus we have a polynomial-time approximation scheme (PTAS) for the number partition problem, though this is not an FPTAS (the running time is exponential in the desired approximation guarantee). However, there are variations of this idea that are fully polynomial-time approximation schemes for the subset-sum problem, and hence for the partition problem as well.[3][4] On the other hand, the problem of minimizing the square of the difference
approximation; thus we have a polynomial-time approximation scheme (PTAS) for the number partition problem, though this is not an FPTAS (the running time is exponential in the desired approximation guarantee). However, there are variations of this idea that are fully polynomial-time approximation schemes for the subset-sum problem, and hence for the partition problem as well.[3][4] On the other hand, the problem of minimizing the square of the difference 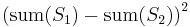 has no FPTAS unless P=NP.[5]
has no FPTAS unless P=NP.[5]
There are also anytime algorithms, based on the differencing heuristic, that first find the solution returned by the differencing heuristic, then find progressively better solutions as time allows (possibly requiring exponential time to reach optimality, for the worst instances).[6]
Hard instances
Sets with 1 or no partitions tend to be hardest (or most expensive) to solve compared to their input sizes. When the values are small compared to the size of the set, perfect partitions are more likely. The problem is known to undergo a "phase transition"; being likely for some sets and unlikely for others. If m is the number of bits needed to express any number in the set and n is the size of the set then 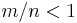 tends to have many solutions and
tends to have many solutions and 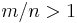 tends to have few or no solutions. As n and m get larger, the probability of a perfect partition goes to 1 or 0 respectively. This was originally argued using methods from physics by Stephan Mertens,[7] and later proved by Borgs, Chayes, and Pittel.[8]
tends to have few or no solutions. As n and m get larger, the probability of a perfect partition goes to 1 or 0 respectively. This was originally argued using methods from physics by Stephan Mertens,[7] and later proved by Borgs, Chayes, and Pittel.[8]
See also
Notes
- ^ a b Hayes 2002
- ^ Karmarkar & Karp 1982
- ^ Hans Kellerer; Ulrich Pferschy; David Pisinger (2004), Knapsack problems, Springer, p. 97, ISBN 9783540402862, http://books.google.com/?id=u5DB7gck08YC&pg=PA97
- ^ Martello, Silvano; Toth, Paolo (1990). "4 Subset-sum problem". Knapsack problems: Algorithms and computer interpretations. Wiley-Interscience. pp. 105–136. ISBN 0-471-92420-2. MR1086874.
- ^ Woeginger, Gerhard J. (2000-01-01), "When Does a Dynamic Programming Formulation Guarantee the Existence of a Fully Polynomial Time Approximation Scheme (FPTAS)?", Informs Journal on Computing 12 (1): 57–74, doi:10.1287/ijoc.12.1.57.11901, http://joc.journal.informs.org/cgi/content/abstract/12/1/57, retrieved 2009-10-05
- ^ Korf 1998, Mertens 1999
- ^ Mertens 1998, Mertens 2001
- ^ Borgs, Chayes & Pittel 2001
References
- Hayes, Brian (May–June 2002), "The Easiest Hard Problem", American Scientist, http://www.americanscientist.org/issues/pub/2002/3/the-easiest-hard-problem
- Karmarkar, Narenda; Karp, Richard M (1982), "The Differencing Method of Set Partitioning", Technical Report UCB/CSD 82/113 (University of California at Berkeley: Computer Science Division (EECS))
- Mertens, Stephan (November 1998), "Phase Transition in the Number Partitioning Problem", Physical Review Letters 81 (20): 4281, Bibcode 1998PhRvL..81.4281M, doi:10.1103/PhysRevLett.81.4281, http://link.aps.org/abstract/PRL/v81/p4281, retrieved 2009-10-03
- Mertens, Stephan (2001), "A physicist's approach to number partitioning", Theoretical Computer Science 265 (1-2): 79–108, doi:10.1016/S0304-3975(01)00153-0
- Mertens, Stephan (2006), "The Easiest Hard Problem: Number Partitioning", in Allon Percus; Gabriel Istrate; Cristopher Moore, Computational complexity and statistical physics, Oxford University Press US, p. 125, arXiv:cond-mat/0310317, ISBN 9780195177374, http://books.google.com/?id=4YD6AxV95zEC&pg=PA125
- Borgs, Christian; Chayes, Jennifer; Pittel, Boris (2001), "Phase transition and finite-size scaling for the integer partitioning problem", Random Structures and Algorithms 19 (3-4): 247–288, doi:10.1002/rsa.10004, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.89.9577, retrieved 2009-10-04
- Korf, Richard E. (1998), "A complete anytime algorithm for number partitioning", Artificial Intelligence 106 (2): 181–203, doi:10.1016/S0004-3702(98)00086-1, ISSN 0004-3702, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.90.993, retrieved 2009-10-04
- Mertens, Stephan (1999), A complete anytime algorithm for balanced number partitioning, arXiv:cs/9903011